Area of Triangles: The area of a triangle or any plane figure is defined as the total space enclosed by their sides . Unit of measurement for area of any plane figure is taken as square metre ( $m^{2}$ ) or square centimetre ( $cm^{2}$

) etc. There are many ways to find the area of a triangle. Heron has derived the famous formula for the area of a triangle in terms of its three sides . Trigonometric functions and determinants are also used to find the area of a triangle .

In this lesson, we will learn the different methods of finding area of triangles, along with some examples.

Different formula for finding area of a triangle:

Contents

Area of Triangles(General Formula)

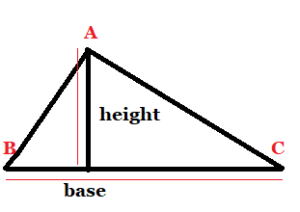
The basic formula for finding the area of triangle is equal to half the product of its base and height. It is applicable to all types of triangles whether it is scalene, isosceles or equilateral.

( fig. 1)

Area of triangle= $\mathbf{\frac{1}{2}\times base \times height}$

When the triangle is right angled ( A triangle in which two sides are perpendicular ) , we can directly apply the formula by using two sides containing the right angle as base and height. For example, suppose that the sides of a right triangle ABC are 8 cm, 15 cm and 17 cm; we take base as 15 cm and height as 8 cm (see Fig. 2), then the area of triangle is given by

$\frac{1}{2}\times base \times height$ = $\frac{1}{2}\times 15\times 8$

=60 $cm^{2}$

(fig. 2)

Note : We could also take 8 cm as the base and 15 cm as height.

How to find area of triangle with 3 sides ?

Area of Scalene Triangle( Heron’s Formula)

A triangle whose all sides are different in length is called scalene triangle. Suppose we know the lengths of the sides of a scalene triangle and not the height. We can still find its area. Heron has derived the formula for the area of a triangle in terms of its three sides. The formula given by Heron about the area of a triangle, is also known as Heron’s formula. It is stated as:

Area of a triangle = $\mathbf{\sqrt{s(s-a)(s-b)(s-c)}}$

where $a$

, $b$ and $c$

are the sides of the triangle and s= semi-perimeter i.e. half of the perimeter of the triangle= $\frac{a+b+c}{2}$ .

This formula is helpful where it is not possible to find the height of the triangle easily.

Example : What is the area of the triangle whose sides are 8 m, 11 m, and 13 m.

Solution : We have $s=\frac{a+b+c}{2}=\frac{8+11+13}{2}=16$

So, $s -a = (16 -8) \,\, cm = 8\, \, cm,$

$s - b = (16 - 11) \, \, cm = 5 \, \, cm,$

$s -c = (16 -13)\, \, cm = 3 \, \, cm.$

Therefore , area of the triangle = $\sqrt{s(s-a)(s-b)(s-c)}$

= $\sqrt{16 \times 8\times 5\times 3}=\sqrt{1920}$

= $8\sqrt{30}\, cm^{2}$

Area of triangle = $8\sqrt{30}\, cm^{2}$ .

How to find the area of an equilateral triangle?

Area of Equilateral triangle

Equilateral triangle is a triangle in which all the three sides are equal also all the three internal angles are equal. The formula for finding area of an equilateral triangle is

Area of an equilateral triangle = $\mathbf{\frac{\sqrt{3}}{4}\times (side)^{2}}$

Derivation for the formula of an equilateral triangle is given below.

Consider the following equilateral triangle ABC whose side length is ‘ $a$ ‘ units. Draw the altitude AD (the perpendicular segment from a vertex of a triangle to the opposite side ) . In an equilateral triangle all its altitude, angle bisector and median from any of its vertices are coincident (they are the same line segment). This can be proved using the concept of congruence of triangles. since AD is median to BC, BD=DC= $\frac{a}{2}$

units.

Now AD is also the perpendicular to BC, we will use the Pythagorean theorem

( $\mathbf{hypotenuse^{2} = base^{2} + height^{2}}$

) to determine its height AD= h units. In triangle ABD,

$AB^{2}=BD^{2}+DA^{2}$

$\Rightarrow a^{2}=(\frac{a}{2})^{2}+h^{2}$

$\Rightarrow h^{2}=a^{2}-\frac{a^{2}}{4}=\frac{3a^{2}}{4}$

$\Rightarrow h=\frac{\sqrt{3}}{2} \, a$

Area of $\Delta ABC$ = $\frac{1}{2}\times base \times height=\frac{1}{2}\times a\times \frac{\sqrt{3}}{2}\, \, a$

= $\frac{\sqrt{3}}{4}\, \, a^{2}$ .

Example : Find the area of an equilateral triangle whose side is $4\sqrt{3}\, \, cm$

Sol. Area of an equilateral triangle = $\mathbf{\frac{\sqrt{3}}{4}\times (side)^{2}}$

= $\frac{\sqrt{3}}{4} \times (4\sqrt{3})^{2}$

= $\frac{\sqrt{3}}{4} \times 48= 12\sqrt{3}\, \, cm^{2}$

Trigonometric formula for finding area of triangles ( Area of triangle with 2 sides and Included angle)

Consider the $\Delta ABC$

, whose vertex angles are ∠ $A$ , ∠ $B$

, and ∠ $C$ , and sides are $a$

, $b$ and $c$

, as shown in the figure below.

Now, if any two sides and the angle between them are given, then the formulas to calculate the area of a triangle is given by:

$Area(\Delta ABC) = \frac{1}{2} \, b\, c\, sin A$

, $Area(\Delta ABC) = \frac{1}{2} \, c\, a\, sin B$ and $Area(\Delta ABC) = \frac{1}{2} \, a\, b\, sin C$

Since AD is perpendicular to BC, In $\Delta ABD$ $\boldsymbol{sin B=\frac{h}{c}}$

$\Rightarrow \boldsymbol{h=c \, sinB}$

Substituting this value of $h$

in the formula Area= $\frac{1}{2}\times \, \, \, base\, \, \times height$ , we get $Area(\Delta ABC) = \frac{1}{2} \, c\, a\, sin B$

.

This is also known as SAS formula for the area of a triangle. Similarly we can write the formula in terms of $\boldsymbol{sin A}$ and $\boldsymbol{sin C}$

also.

Example: In $\Delta ABC$ , $\angle A = 30^{\circ}$

, side $b = 6$ units, side $c$

= 8 units.

$Area(\Delta ABC) = \frac{1}{2} \, b\, c\, sin A$

$= \frac{1}{2} \times 6 \times 8 \,\times sin 30^{\circ}$

= $24 \times \frac{1}{2} \, \, (since\, \, sin \, 30^{\circ}$ = $\frac{1}{2}$

)

$=12\, \, square\, units$

Area $\Delta ABC$

= 12 square units.

Area of triangles formula using determinant

Let $(x_{1},y_{1}), (x_{2},y_{2})$ and $(x_{3},y_{3})$

be the co Area of a triangle with vertices $(x_{1},y_{1}), (x_{2},y_{2})$ and $(x_{3},y_{3})$

is given by

$\Delta =\frac{1}{2}\begin{vmatrix} & x_{1} &y_{1} & 1\\ &x_{2} &y_{2} & 1\\ &x_{3} &y_{3} &1 \end{vmatrix}$

Note: 1. Since area is a positive quantity , we always take the absolute value of the determinant in finding the area of triangle.

2. If area is given , use both positive and negative values of the determinant for calculation.

3. The area of triangle formed by three collinear points is zero.

Example: Find the area of the triangle whose vertices are (3,8), (-4, 2) and (5,1) .

Sol. Area of a triangle with vertices $(x_{1},y_{1}), (x_{2},y_{2})$

and $(x_{3},y_{3})$ is given by

$\Delta =\frac{1}{2}\begin{vmatrix} & x_{1} &y_{1} & 1\\ &x_{2} &y_{2} & 1\\ &x_{3} &y_{3} &1 \end{vmatrix}$

Putting the given values, area of the triangle is $\Delta$ = $\frac{1}{2}\begin{vmatrix} 3& 8 & 1&\\ -4& 2& 1&\\ 5& 1& 1& \end{vmatrix}$

= $\frac{1}{2}[3(2-1)-8(-4-5)+1(-4-10)]$

= $\frac{1}{2}(3+72-14)=\frac{61}{2}$

sq. units

Area of triangles quizzes

Created on September 26, 2021

Triangle Quizzes

1 / 5

The base of a right angled triangle is 8 cm and hypotenuse is 17 cm. Find its area.

15 square cm

21 square cm

18 square cm

60 square cm

2 / 5

2. Find the area of an equilateral triangle whose side is $4\sqrt{3}$

cm.

12 \sqrt{3} cm^{2}

14 \sqrt{3} cm^{2}

115 \sqrt{3} cm^{2}

30 \sqrt{3} cm^{2}

3 / 5

3. Find the area of an isosceles triangle whose equal sides are 5 cm each and the base is 6 cm.

12 cm^{2}

6 cm^{2}

9 cm^{2}

15 cm^{2}

4 / 5

4. Find the area of an equilateral triangle with side 10 cm.

25 \sqrt(3) square cm

25 square cm

5 \sqrt(3) square cm

20 \sqrt(3) square cm

5 / 5

Find the area of the given triangle.

15 square cm

12 square cm

10 square cm

24 square cm

Your score is

The average score is 70%

Also read :

Basic Trigonometric identities : < http://mathmitra.com/trigonometric-identities/ >
Mensuration Formula for 2D and 3D shapes : <http://mathmitra.com/mensuration-formulas/>

Area of Triangles- Definition, Formula and Examples

Area of Triangles(General Formula)

Area of Scalene Triangle( Heron’s Formula)

Area of Equilateral triangle

Trigonometric formula for finding area of triangles ( Area of triangle with 2 sides and Included angle)

Area of triangles formula using determinant

Bina singh

Leave a Reply Cancel reply

Area of Triangles(General Formula)

Area of Scalene Triangle( Heron’s Formula)

Area of Equilateral triangle

Trigonometric formula for finding area of triangles ( Area of triangle with 2 sides and Included angle)

Area of triangles formula using determinant

Bina singh

You might also like

Prime Factors and Pair Factors of 160

Class 8 maths chapter 1 exercise 1.2 solutions

Factoring trinomials worksheet

Find factors of a number (Definition, Properties, Formulas and Examples)

Various types of numbers: natural numbers, whole numbers, integers and rational numbers

Leave a Reply Cancel reply