Trigonometric identities are formulas that involve Trigonometric functions. Trigonometry is a branch of mathematics that deals with the study of relationships between lengths and angles of triangles. The early applications of the trigonometric functions were to surveying, navigation, and engineering. These functions also play an important role in the study of all sorts of vibratory phenomena-sound, light, electricity, etc.

Contents

Trigonometric Ratios

Let us take a right triangle ABC as shown below.

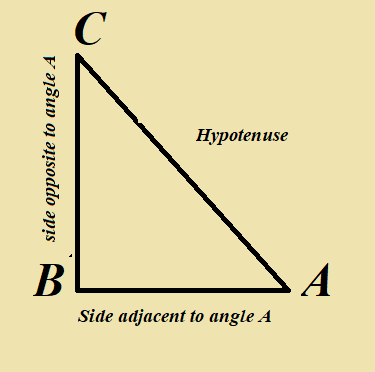
define trignometric ratio — Right angle triangle ABC

The trigonometric ratios of the angle A in right triangle ABC are defined as follows :

$\boldsymbol{\mathrm{sin}}A= \frac{side \, \, opposite \, \, to \, \, angleA}{hypotenuse}=\frac{BC}{CA}$

$\boldsymbol{\mathrm{cos}}A= \frac{side \, \, adjacent \, \, to \, \, angleA}{hypotenuse}=\frac{AB}{AC}$

$\boldsymbol{\mathrm{tan}}A= \frac{side \, \, opposite \, \, to \, \, angleA}{side \, \, adjacent \, \, to\, \, angle\, A}=\frac{BC}{AB}$

$\boldsymbol{\mathrm{cosec A}}=\frac{1}{\mathrm{sin}A}=\frac{hypotenuse}{side\, \, opposite \, \, to \, \, angle A}=\frac{AC}{BC}$

$\boldsymbol{\mathrm{sec A}}=\frac{1}{\mathrm{cos}A}=\frac{hypotenuse}{side\, \, adjacent \, \, to \, \, angle A}=\frac{AC}{AB}$

$\boldsymbol{\mathrm{cot A}}=\frac{1}{\mathrm{tan}A}=\frac{side \, \, adjacent \, \, to\, \, angle \, A}{side\, \, opposite \, \, to \, \, angle A}=\frac{AB}{BC}$

Note that the ratios cosec A, sec A and cot A are respectively, the reciprocals of the ratios sin A, cos A and tan A. So, the trigonometric ratios of an acute angle in a right triangle express the relationship between the angle and the length of its sides. These are trigonometric ratios for with respect to acute angle A. However, these ratios can be extended to other angles also.

Trigonometric ratios of some specific angles

$\mathbf{\angle A}$	$\mathbf{0^{\circ}}$	$\mathbf{30^{\circ}}$	$\mathbf{45^{\circ}}$	$\mathbf{60^{\circ}}$	$\mathbf{90^{\circ}}$
$\mathbf{{\color{Red} sinA}}$	$\mathbf{}$ $\mathbf{0}$	$\mathbf{\frac{1}{2}}$	$\mathbf{\frac{1}{\sqrt{2}}}$	$\mathbf{\frac{\sqrt{3}}{2}}$	$\boldsymbol{1}$
$\mathbf{{\color{Red} cosA}}$	$\mathbf{1}$	$\mathbf{\frac{\sqrt{3}}{2}}$	$\mathbf{\frac{1}{\sqrt{2}}}$	$\mathbf{\frac{1}{2}}$	$\mathbf{0}$
$\mathbf{{\color{Red} tanA}}$	$\mathbf{0}$	$\mathbf{\frac{1}{\sqrt{3}}}$	$\mathbf{1}$	$\mathbf{\sqrt{3}}$	not defined
$\mathbf{{\color{Red} cosecA}}$	not defined	2	$\mathbf{\sqrt{2}}$	$\mathbf{\frac{2}{\sqrt{3}}}$	$\mathbf{1}$
$\mathbf{{\color{Red} secA}}$	$\mathbf{1}$	$\mathbf{\frac{2}{\sqrt{3}}}$	$\mathbf{\sqrt{2}}$	2	not defined
$\mathbf{{\color{Red} cotA}}$	not defined	$\mathbf{\sqrt{3}}$	$\mathbf{1}$	$\mathbf{\frac{1}{\sqrt{3}}}$	0

Remark : From the table above you can observe that as ∠ A increases from 0° to 90°, sin A increases from 0 to 1 and cos A decreases from 1 to 0.

Trigonometric Ratios of Complementary Angles

$\mathbf{sin(90^{\circ}-A) = cos A,}$

$\mathbf{cos(90^{\circ}-A) = sin A,}$
$\mathbf{tan(90^{\circ}-A) = cot A,}$

$\mathbf{cot(90^{\circ}-A) = tan A,}$
$\mathbf{sec(90^{\circ}-A) = cosec A,}$

$\mathbf{cosec(90^{\circ}-A) = sec A,}$

Trigonometric Identities

An equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true for all values of the angle(s) involved. Some basic trigonometric identities are :

(i) $\mathbf{sin^{2}A+cos^{2}A=1 \, \, \, \, (0^{\circ}\leq A\leq 90^{\circ})}$

(ii) $\mathbf{1+tan^{2}A=sec^{2}A\, \, \, \, \, \, (0^{\circ}\leq A< 90^{\circ})}$

(iii) $\mathbf{cot^{2}A+1=cosec^{2}A\, \, \, \, \, \, \, (0^{\circ}< A\leq 90^{\circ})}$

These are the trigonometric ratios of acute angles as the ratio of the sides of a right angled triangle. Further the concept of trigonometric ratios is extended to the trigonometric ratios to any angle in terms of radian measure and study them as trigonometric functions.

Trigonometric functions

Consider a unit circle with centre 0. In right angle triangle OMP , $\mathbf{\mathrm{cos \theta =\mathrm{a}}}$

and $\mathbf{\mathrm{sin \theta =\mathrm{b}}}$ . Since

triangle OMP is a right triangle , we have $(OM)^{2}+(MP)^{2}=(OP)^{2}$

$\Rightarrow a^{2}+b^{2}=1$

$\bg_white \large \Rightarrow \mathbf{\mathrm{{\color{DarkBlue} cos^{2}\theta +sin^{2}\theta =1}}}$

Now, if we take one complete revolution from the point P, we again come back to
same point P. Thus, we also observe that if $\bg_white \large \theta$ increases (or decreases) by any integral
multiple of $\bg_white \large 2\pi$

, the values of sine and cosine functions do not change. Thus,

$\bg_green \large\mathbf{\mathrm{sin(2n\pi +\theta )=sin\theta }}\, \, \, \mathrm{n\in \mathbb{Z}}$ and $\bg_green \large \bg_green \large\mathbf{\mathrm{cos(2n\pi +\theta )=cos\theta }}\, \, \, \mathrm{n\in \mathbb{Z}}$

Further

$\bg_white \large \mathbf{\mathrm{sin\theta =0}}$ , if $\bg_white \large \theta =0,\pm \pi , \pm 2\pi,\pm 3\pi,\pm 4\pi.......$

i.e. when $\bg_white \large \theta$ is an integral multiple of $\bg_white \large \pi$

and

$\bg_white \large \mathbf{\mathrm{cos\theta =0}}$ , if $\bg_white \large \theta =\pm \frac{\pi }{2}, \pm \frac{3\pi }{2},\pm \frac{5\pi }{2},\pm \frac{7\pi }{2},........$

, i.e. $\bg_white \large cos\theta$ vanishes when $\bg_white \large \theta$

is an odd multiple of $\bg_white \large \frac{\pi }{2}$

Thus $\bg_green \large \mathbf{\mathrm{sin\theta =0 \, \, implies\, \, \theta =n\pi , \, \, where\, n\, is \, any \, integer}}$

and

$\bg_green \large \mathbf{\mathrm{cos\theta =0, \, \, implies\, \, \theta =(2n+1)\frac{\pi }{2}}}, \, where \, \, n\, is \, any \, \, integer$

Other trigonometric functions are

$\bg_white \large \mathbf{\mathrm{cosec\theta =\frac{1}{sin\theta }}}$

, $\bg_white \large \theta \neq n\pi$ , where $\bg_white \large n$

is any integer

$\bg_white \large \bg_white \large \mathbf{\mathrm{sec\theta =\frac{1}{cos\theta }}}$ , $\bg_white \large \theta \neq (2n+1)\frac{\pi }{2}$

, where $\bg_white \large n$ is any integer

$\bg_white \large \mathbf{\mathrm{tan\theta =\frac{sin\theta }{cos\theta }}}$

, $\bg_white \large \theta \neq (2n+1)\frac{\pi }{2}$ , where $\bg_white \large n$

is any integer

$\bg_white \large \mathbf{\mathrm{cot\theta }=\frac{cos\theta }{sin\theta }}$ , $\bg_white \large \theta \neq n\pi$

, where $\bg_white \large n$ is any integer

Therefore we have the following identities

$\bg_white \large \mathbf{\mathrm{sin^{2}\theta +cos^{2}\theta =1 , \, \, \forall \, \, \theta \in \mathbb{R}}}$

$\bg_white \large 1+\mathbf{\mathrm{tan^{2}\theta =sec^{2}\theta , \, \forall \, \theta \, \in \mathbb{R}-\{(2n+1)\frac{\pi }{2}|n \in \mathbb{Z}\}}}$

$\bg_white \large \bg_white \large 1+\mathbf{\mathrm{cot^{2}\theta =cosec^{2}\theta , \, \forall \, \theta \, \in \mathbb{R}-\{n\pi |n \in \mathbb{Z}\}}}$

Trigonometric ratios of higher angles:

Degree	$\bg_white \large 0^{\circ}$	$\bg_white \large 30^{\circ}$	$\bg_white \large 45^{\circ}$	$\bg_white \large 60^{\circ}$	$\bg_white \large 90^{\circ}$	$\bg_white \large 180^{\circ}$	$\bg_white \large 270^{\circ}$	$\bg_white \large 360^{\circ}$
Radian	$\bg_white \large 0$	$\bg_white \large \frac{\pi }{6}$	$\bg_white \large \frac{\pi }{4}$	$\bg_white \large \frac{\pi }{3}$	$\bg_white \large \frac{\pi }{2}$	$\bg_white \large \pi$	$\bg_white \large \frac{3\pi }{2}$	$\bg_white \large 2\pi$
sin	0	$\mathbf{\frac{1}{2}}$	$\bg_white \large \frac{1}{\sqrt{2}}$	$\bg_white \large \frac{\sqrt{3}}{2}$	1	0	-1	0
cos	1	$\bg_white \large \frac{\sqrt{3}}{2}$	$\bg_white \large \frac{1}{\sqrt{2}}$	$\mathbf{\frac{1}{2}}$	0	-1	0	1
tan	0	$\bg_white \large \frac{1}{\sqrt{3}}$	1	$\bg_white \large \sqrt{3}$	not defined	0	not defined	0
cot	not defined	$\bg_white \large \sqrt{3}$	1	$\bg_white \large \frac{1}{\sqrt{3}}$	0	not defined	0	not defined
sec	1	$\bg_white \large \frac{2}{\sqrt{3}}$	$\bg_white \large \sqrt{2}$	2	not defined	-1	not defined	1
cosec	not defined	2	$\bg_white \large \sqrt{2}$	$\bg_white \large \frac{2}{\sqrt{3}}$	1	not defined	-1	not defined

Sign of trigonometric functions in different quadrants:

	I	II	III	IV
$\bg_white \large \mathbf{\mathrm{sin\theta }}$	+	+	–	–
$\bg_white \large \mathbf{\mathrm{cos\theta }}$	+	–	–	+
$\bg_white \large \mathbf{\mathrm{tan\theta }}$	+	–	+	–
$\bg_white \large \mathbf{\mathrm{cosec\theta }}$	+	+	–	–
$\bg_white \large \mathbf{\mathrm{sec\theta }}$	+	–	–	+
$\bg_white \large \mathbf{\mathrm{cot\theta }}$	+	–	+	–

Note: The signs (positive or negative) of the trigonometric ratios in the four quadrants can be remembered as
shown below.

I	II	III	IV
All	Silver	Tea	Cups

In quadrant I, all are positive.
In quadrant II, only sine (and its reciprocal cosec) is positive.
In quadrant III, only tangent (and its reciprocal cot) are positive.
In quadrant IV, only cosine (and its reciprocal sec) is positive.

Trigonometric Functions of Sum and Difference of Two Angles

$\bg_white \large cos (\alpha + \beta ) = cos\alpha \, cos \beta - sin \alpha \, sin \beta$
$\bg_white \large cos (\alpha - \beta ) = cos\alpha \, cos \beta + sin \alpha \, sin \beta$
$\bg_white \large sin (\alpha + \beta )=sin \alpha\, \, cos \beta+ cos \alpha \,\, sin \beta$
$\bg_white \large \bg_white \large sin (\alpha - \beta ) = sin \alpha \, \, cos \beta -cos \alpha \, \, sin \beta$
If none of the angles $\alpha ,\beta$ and $\bg_white \large (\alpha +\beta )$ is an odd multiple of $\bg_white \large \frac{\pi }{2}$ , then $\bg_white \large tan(\alpha +\beta )=\frac{tan\alpha +tan\beta }{1-tan\alpha \, \, tan\beta }$
If none of the angles $\alpha ,\beta$ and $\bg_white \large (\alpha -\beta )$ is an odd multiple of $\bg_white \large \frac{\pi }{2}$ , then $\bg_white \large tan(\alpha -\beta )=\frac{tan\alpha -tan\beta }{1+tan\alpha \, \, tan\beta }$

If none of the angles $\alpha ,\beta$ and $\bg_white \large (\alpha +\beta )$ is a multiple of $\pi$ , then $\bg_white \large cot(\alpha +\beta )=\frac{cot\alpha \, \,cot\beta -1 }{cot\alpha +cot\beta }$

If none of the angles $\alpha ,\beta$ and $\bg_white \large (\alpha -\beta )$ is a multiple of $\pi$ , then $\bg_white \large cot(\alpha -\beta )=\frac{cot\alpha \, \,cot\beta +1 }{cot\beta -cot\alpha }$
$\bg_white \large cos\, 2\alpha =cos^{2}\alpha -sin^{2}\alpha =2cos^{2}\alpha -1=1-2sin^{2}\alpha$

$\bg_white \large cos2\alpha =\frac{1-tan^{2 }\alpha }{1+tan^{2}\alpha }, \alpha \neq n\pi +\frac{\pi }{2}, n \, \, is\, an \, integer$

$\bg_white \large sin2\alpha =2sin\alpha\, cos\alpha$

$\bg_white \large sin2\alpha =\frac{2tan\alpha }{1+tan^{2}\alpha }, \alpha \neq n\pi +\frac{\pi }{2}, n \, \, is\, an \, integer$

$\bg_white \large tan2\alpha =\frac{2tan\alpha }{1-tan^{2}\alpha }$ , if $\bg_white \large 2\alpha \neq n\pi +\frac{\pi }{2}$ , n is an integer

$\bg_white \large sin 3\alpha = 3 sin \alpha - 4 sin^{3} \alpha$
$\bg_white \large cos 3\alpha = 4 cos^{3} \alpha - 3 cos \alpha$

$\bg_white \large tan3\alpha =\frac{3tan\alpha -tan^{3}\alpha }{1-tan^{3}\alpha }, 3\alpha \neq n\pi +\frac{\pi }{2}$ where n is an integer

$\bg_white \large cos\alpha+cos\beta =2cos\frac{\alpha +\beta }{2}cos\frac{\alpha -\beta}{2}$

$\bg_white \large \bg_white \large cos\alpha-cos\beta =-2sin\frac{\alpha +\beta }{2}sin\frac{\alpha -\beta}{2}$

$\bg_white \large \bg_white \large sin\alpha+sin\beta =2sin\frac{\alpha +\beta }{2}cos\frac{\alpha -\beta}{2}$

$\bg_white \large \bg_white \large sin\alpha-sin\beta =2cos\frac{\alpha +\beta }{2}sin\frac{\alpha -\beta}{2}$
$\bg_white \large 2 cos \alpha \, cos \beta = cos (\alpha + \beta ) + cos (\alpha -\beta )$
$\bg_white \large -2 sin \alpha sin \beta = cos (\alpha + \beta ) -cos (\alpha - \beta )$
$\bg_white \large 2 sin \alpha \, cos \beta = sin (\alpha + \beta ) + sin (\alpha - \beta )$
$\bg_white \large 2 cos \alpha \, sin \beta = sin (\alpha + \beta ) - sin (\alpha - \beta )$