Cardinality Of A Set And Practical Problems Based On Sets

Cardinality of a set : cardinality of a set, which is basically the size of the set. The cardinality of a set is denoted by $\small \left | A \right |$ . For finite sets , cardinality is simply the number of distinct elements in $A$

For example, if $\small A=\left \{ 2,4,6,8,10 \right \}$ , then $\small \left | A \right |$ =5.

Important results on numbers of elements in sets:

Let $A$ , $B$ and $C$ be any finite sets and and $\small U$ be the finite universal set, then

(a) $n(A\cup B)=n(A)+n(B)-n(A\cap B)$

(b) If $A\cap B=\phi ,$ then $n(A\cup B)=n(A)+n(B)$

(d) $\small n(A-B)=n(A)-n(A\cap B)\, \, i.e.\, \, n(A-B)+ n(A\cap B)=n(A)$

(e) $\small n({A}'\cup {B}')=n({(A\cap B)}')=n(U)-n(A\cap B)$

(f) $\small n({A}'\cap {B}')=n({(A\cup B)}')=n(U)-n(A\cup B)$

(g) Number of elements which belong to exactly one of $\small A$ or $\small B$ = $\small n(A)+n(B)-2n(A\cap B)$

(h) Number of elements in exactly two of the sets $\small A,\, B, \, C$ = $\small n(A\cap B)+n(B\cap C)+n(C\cap A)-3n(A\cap B\cap C)$

(i) Number of elements in exactly one of the sets $\small A,\, B, \, C$

= $\small n(A)+n(B)+n(C)-2n(A\cap B)-2n(B\cap C)-2n(A\cap C)+3n(A\cap B\cap C)$

practical problems based on sets:

Example 1. Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science,
6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and
Science; 4 in all the three. Find how many passed
(i) in English and Mathematics but not in Science
(ii) in Mathematics and Science but not in English
(iii) in Mathematics only
(iv) in more than one subject only

Sol. Let $\small M$ be the set of students who passed in Mathematics, $\small E$ be the set of students who passed in English and $\small S$ be the set of students who passed in Science. Given

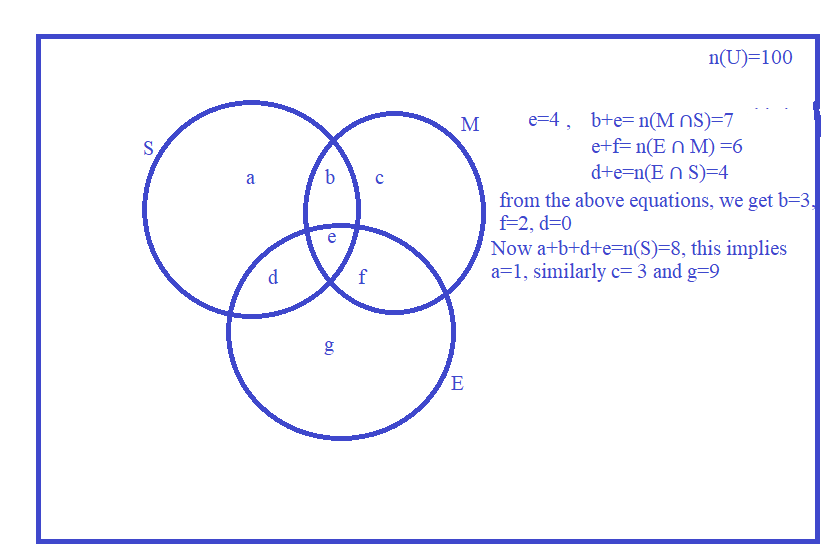
$\small n(U)=100$ , $\small n(E)=15$ , $\small n(M)=12$ , $\small n(S)=8$ , $\small n(E\cap M)=6$ , $\small n(M\cap S)=7$ , $\small n(E\cap S)=4$ , $\small n(M\cap E\cap S)=4$

Number of students passed in English and Mathematics but not in Science = f = 2
(ii) Number of students passed in Mathematics and Science but not in English = b = 3
(iii) Number of students passed in Mathematics only = c = 3
(iv) Number of students passed in more than one subject = b + d + e + f =3+0+4+2=9

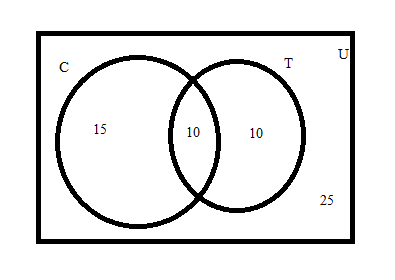
Example 2. In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Find the number of students who play neither?

Solution: let $\small C$ be the set of students who play cricket , $\small T$ be the set of students who play tennis and total students represent universal set $\small U$ , then according to the question

$\small n(U)=60$ , $\small n(C)=25$ , $\small n(T)=20$ and $\small n(C\cap T)=10$

We have to find the number of students who play neither means we to find the $\small n({(C\cup T)}')$ (shaded portion in the venn diagram given below).