November 20, 2024

Remainder Theorem

by Bina singhDecember 28, 2020October 6, 2022

Remainder theorem

Zeros of polynomials:

The value of a polynomial at

is obtained by putting

in

and is denoted by .

e.g. Find the value of $p(x)=x^{2}-5x+6$ at

.

Sol. On putting in given polynomial , we get

$p(-1)=(-1)^{2}-5(-1)+6=1+5+6$

This implies .

Thus value of

at

is 12.

We say that a zero of a polynomial

is a number $\large c$ such that

. It means $\large c$ is zero of a polynomial

if the value of that polynomial at $\large c$ is zero.

The zeros of polynomials is obtained by equating the given polynomial

. We say $p\left ( x \right )=0$ is a polynomial equation and $c$

is root of the polynomial equation $p\left ( x \right )= 0$ .

Let $p\left ( x \right )=a$

be a constant polynomial, then $p\left ( x \right )=ax^{0}$ .

Now replace $x$

with any number we still get $p\left ( x \right )=a$ . This implies constant polynomials has no zeros. In case of zero polynomial , every real number is a zero of the zero polynomial.

Important observations:

(i) Every linear polynomial has one and only one zero.

Let $\large p(x)=ax+b, \, a\neq 0$

be a linear polynomial,

then means

.

$\Rightarrow x=-\frac{b}{a}$

So $x=-\frac{b}{a}$

is the only zero of

.

i.e. a linear linear polynomial has one and only one zero.

(ii) A zero of polynomial need not be 0.

e. g. The zeros of $p(x)=x^{2}-4$

are -2 and 2.

(iii) 0 may be a zero of polynomial.

e.g. Take

(iv) A polynomial can have more than one zero.

Division algorithm in polynomials:

When we divide two numbers, we always get

Dividend =(divisor x quotient)+remainder, where $0\leq remainder< divisor$

. When remainder becomes zero, we say divisor and quotient both are factors of dividend.

Now, let two polynomials $p(x)=3x^{4}-4x^{3}-3x-2$ and $g(x)=x-2$

. Divide $p(x)$ by $g(x)$

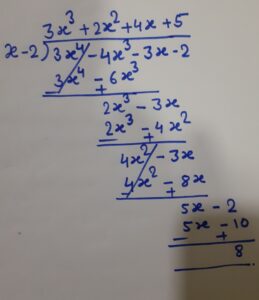
{ Steps to divide a polynomial by a non-zero polynomial

First, arrange the polynomials (dividend and divisor) in the decreasing order of its degree
Divide the first term of the dividend by the first term of the divisor to produce the first term of the quotient
Multiply the divisor by the first term of the quotient and subtract this product from the dividend, to get the remainder.
This remainder is the dividend now and divisor will remain same
Again repeat from the first step, until the degree of the new dividend is less than the degree of the divisor.}

Now $(x-2)(3x^{3}+2x^{2}+4x+5)+8= 3x^{4}+2x^{3}+4x^{2}+5x-6x^{3}-4x^{2}-8x-10+8$

$\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, = 3x^{4}-4x^{3}-3x-2$

$\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, =p(x)$

Hence $p(x)=g(x)\times q(x)+r(x)$ where $deg(r(x))=0< 1=deg(g(x))$

.

In general , If $p(x)$ and $g(x)$

are two polynomials such that $deg(p(x))\geq deg(g(x))$ and $g(x)\neq 0$

, then we can find a polynomial $q(x)$ as quotient and $r(x)$

as remainder, where $r(x)=0$ or $deg(r(x))< deg(g(x))$

.

In the above example the divisior is a linear polynomial . In such a situation there is a way to find the remainder called Remainder Theorem.

Remainder theorem

Let $p(x)$ be any polynomial of degree greater than or equal to one and let $\large a$

be any real number. If $p(x)$ is divided by the linear polynomial $x-a$

, then remainder is $p(a)$ .

Proof. Let $p(x)$

be any polynomial of degree greater than or equal to 1. Suppose $p(x)$ is divided by $(x-a)$

then by using division algorithm theorem , $p(x)$ can be written as

$\, \, \, \, \, \, \, \, \, \, \, \, \, \, p(x)=(x-a)q(x)+r(x)$

since degree of $r(x)<$ degree of $q(x)$

, this implies degree of $r(x)$ =0 ( $\because$

degree of $q(x)=1$ )

$\Rightarrow r(x)=c$

(a constant polynomial)

$\Rightarrow p(x)=(x-a)q(x)+c$

In particular if $x=a$

then $p(a)=c,$ which proves the theorem.

e.g. Find the remainder when $x^{5}+x^{4}-2x^{3}+x^{2}+1$

is divided by $(x-1)$ .

Sol. Here $p(x)=x^{5}+x^{4}-2x^{3}+x^{2}+1$

and zeros of $x-1$ is 1.

so $p(1)=(1)^{5}+(1)^{4}-2(1)^{3}+(1)^{2}+1$

$=1+1-2+1+1$

= $2$

Hence by the remainder theorem , the remainder is 2.

Also Read:

Bina singh

View all posts by Bina singh →

Leave a Reply Cancel reply