Definite Integration Involving Modulus Function

There is no anti-derivative for a modulus function; however we know it’s definition

$\left | x \right |= \left\{\begin{matrix} x\, \, if \, \, x\geq 0\\ -x \, \, otherwise \end{matrix}\right.$

Thus we can split up our integral in two parts. One part must be completely negative and the another must be completely positive. This strategy is known as splitting . To split correctly it is better to draw the modulus graph so that we can get the correct equation to represent each portion of the modulus graph .

Example 1. Find the value of $\int_{\pi }^{10\pi }\left | sin x \right |dx$

Sol. For a periodic function $f(x)$ with period $T$ , $\int_{a}^{a+nT}f(x)dx=n\int_{0}^{T}f(x)dx$ , where $n$ is any natural number.

Here $f(x)=\left | sinx \right |$ whose period is $\pi$ .

Hence $\int_{\pi }^{10\pi }\left | sin x \right |dx=\int_{\pi }^{\pi+9\pi }\left | sin x \right |dx= 9\int_{0}^{\pi}\left | sin x \right | dx$

= $9\int_{0}^{\pi }sin x \, dx$ ( since $sinx \geq 0, \forall \, \, x\in [0,\, \pi ]$ )

= $9{\left [ -cosx \right]}_{0}^{\pi }$ = 9 x 2 =18 .

Thus $\int_{\pi }^{10\pi }\left | sin x \right |dx= 18$

Example 2. Evaluate $\int_{-1}^{2}\left | x^{3} -x\right |dx$

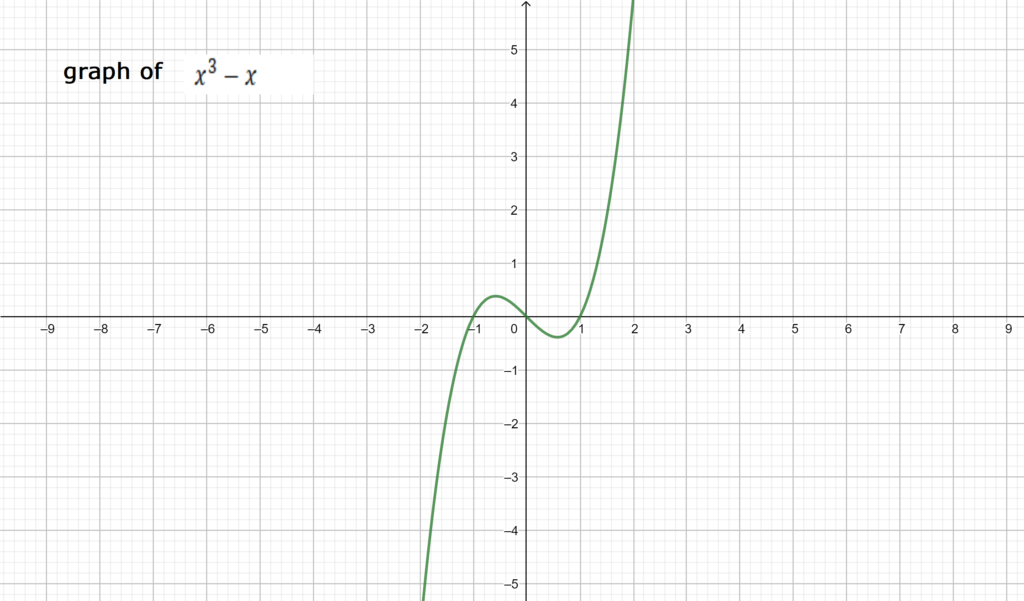
Sol. We note that $x^{3}-x\geq 0$ on $\left [ -1, \, 0 \right ]$ and $x^{3}-x\leq 0$ on $\left [ 0, \, 1\right ]$ and that $x^{3}-x\geq 0$ on $\left [ 1, 2 \right ]$ .

Graph of $x^{3}-x$

So $\int_{-1}^{2}\left |x^{3} -x\right|dx=\int_{-1}^{0}(x^{3}-x)dx+\int_{0}^{1}-(x^{3}-x)dx+\int_{1}^{2}(x^{3}-x)dx$

= $\int_{-1}^{0}(x^{3}-x)dx+ \int_{0}^{1}(x-x^{3})dx+ \int_{1}^{2}(x^{3}-x)dx$

= $\left [ \frac{x^{4}}{4}-\frac{x^{2}}{2} \right ]_{-1}^{0}+\left [ \frac{x^{2}}{2}-\frac{x^{4}}{4} \right ]_{0}^{1}+\left [ \frac{x^{4}}{4}-\frac{x^{2}}{2}\right ]_{1}^{2}$

= $-(\frac{1}{4}-\frac{1}{2})+(\frac{1}{2}-\frac{1}{4})+(4-2)-(\frac{1}{4}-\frac{1}{2})$

= $\frac{11}{4}$

Example 3. Find the value $\int_{0}^{\frac{\pi }{2}}\left | cosx-sinx \right |dx$

Sol. We know that $sin\, x$ and $cos\, \, x$ has one common value at $x=\frac{\pi }{4}$ . In the interval $\left [ 0,\, \frac{\pi}{4} \right ]$ , $cos\, x\geq sin\, x$ and in $\left [ \frac{\pi }{4} , \, \frac{\pi }{2}\right ]$ , $sin\, x\geq cos\, x$ . Thus $cosx-sinx \geq 0$ in $\left [ 0,\, \frac{\pi}{4} \right ]$ and $cosx-sinx \leq 0$ in $\left [ \frac{\pi }{4} , \, \frac{\pi }{2}\right ]$ .

So $\int_{0}^{\frac{\pi }{2}}\left | cosx-sinx \right |dx=\int_{0}^{\frac{\pi }{4}}\left ( cosx-sinx \right )dx+\int_{\frac{\pi }{4}}^{\frac{\pi }{2}}-\left ( cosx-sinx \right )dx$