by Factoring Polynomials Formula and Factoring Polynomials Worksheet with Answers
What is Factorisation?
Representation of an algebraic expression ( polynomials )as the product of two or more expressions is called factorisation. Each such expression is called a factor of the given algebraic expression. These factors may be numbers, algebraic variables or algebraic expressions.
 |
 |
 |
When the factors of the polynomial are multiplied together, you will get the original polynomial.
Methods of Factoring Polynomials
There are a certain number of methods by which we can factorise polynomials. Let us discuss these methods.
(i) Method of common factors
The first method for factoring polynomials will be factoring out the greatest common factor. It means look at all the terms and determine if there is a factor that is in common to all the terms. If there is, we will factor it out of the polynomial. For example ,Suppose we have to factorise
Now the distributive law states that a(b+c) = ab + bc . By using this law
Therefore, we can write
Note that we can always check our factoring by multiplying the terms back out to make sure we get the original polynomial.
Let’s take a look at some more examples.
Example 1: Factorise .
Solution :
Thus the common factors are and
Therefore
Answer: Thus the factors of are
Example 2 : Factorise
Solution:
Thus the common factors are 3 , 3 and i.e. 9y.
Therefore
Answer: The factors of are
Example 3: Factorise
Solution:
Thus the common factors are 3, a, b and c i.e. 3abc.
Therefore
Answer: Thus the factors of are
Example 4: Factorise
Solution :
Thus the common factors are and
Therefore
Answer : Factors of are
(ii)Factoring By Grouping
Let us try to understand grouping for factorizing with the help of the following examples.
Example 1: Factorize the polynomial using the method of regrouping of factoring a polynomial.
Solution: For factoring polynomials we observe that we have no common factor among all the terms in the expression
Answer: Therefore the factors of
Example 2: Factorise
Solution: There is no common factor among all the terms. Notice that first two terms have a common factor
terms have common factor 1.
So,
=
The factors of
Example 3 : Factorise
Solution: There is no common factors in all the terms of
=
Hence, the required factors are
Example 4: Factorise
Solution: Grouping the terms, we have
Hence, the required factors = and
Example 5: Factorise .
Solution:
=
=
Thus the required factors are
(iii) Factorisation using Algebraic Identities (Factoring Polynomials Formulas)
There are some nice special forms of some polynomials that can make factoring easier for us. Some of them are given below.
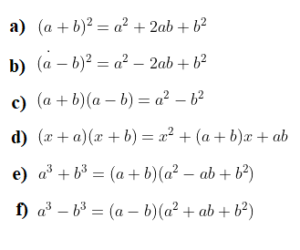
Example 1: Factorise .
Sol. The polynomial
Now using the identity
.
Example 2: Factorise
Solution: can be written as
Now using the identity
=
Example 3: Factorise .
Solution:
The expression is of the form where
Now using the identity
=
Now, cannot be factorised further, but (
Again using the same identity , it follows that
.
Answer : Therefore the factors of
Example 4: Factorise
Solution:
=
= [Applying Identity
Answer : Thus the factors of are
Example 5: Factorise
Solution: .
The expression is of the form
Now applying the identity , we get
Answer : Therefore the factors of are
Example 6: Factorise
Solution : . Now using the identity
we get .
Answer : Factors of
Factoring polynomial worksheet PDF
You might also be interested in:
- Polynomials : Definition, Types of polynomials and Examples, Degree of a polynomial
- Relationship between Zeros and coefficients of a Polynomial
- Polynomials Worksheet Grade 9 with PDF
