NCERT Class 8 Maths Chapter Square And Square Roots

Class 8 Maths Chapter Square and Square Roots (Exemplar Solution)

Understanding squares and square roots is an important part of learning mathematics in Class 8. These concepts help build a strong foundation for more advanced math topics you’ll encounter later. The NCERT Class 8 Maths Exemplar provides various problems to help students practice and understand these concepts better. In this blog, we have simple and clear solutions to these problems, making it easier for you to learn and solve them.

In each of the questions, 1 to 24, write the correct answer from the given four options.
1. 196 is the square of
(a) 11 (b) 12 (c) 14 (d) 16
Ans. (c)
Since $14\times 14=196$ , this implies 196 is square of 14.

2. Which of the following is a square of an even number?
(a) 144 (b) 169 (c) 441 (d) 625
Ans.(c)
Square of an even number ends with an even number. So 144 is a square of an even number.
12 x 12 =144.

3. A number ending in 9 will have the units place of its square as
(a) 3 (b) 9 (c) 1 (d) 6
Ans. (c) Example : 9x 9 =81 , 19 x 19= 361 etc.

4. Which of the following will have 4 at the units place?
(a) $14^{2}$

(b) $62^{2}$ (c) $27^{2}$ (d) $35^{2}$
Ans. (b) Since $class 8 maths chapter square and square roots$

5. How many natural numbers lie between $5^{2}$ and $6^{2}$ ?
(a) 9 (b) 10 (c) 11 (d) 12
Ans. (b)Since there are ‘2n’ natural numbers between n and ( n+1). So there are 2 x 5=10 natural numbers between $5^{2}$ and $6^{2}$ .

6. Which of the following cannot be a perfect square?
(a) 841 (b) 529 (c) 198 (d) All of the above
Ans. (c) A number ending with digits 2, 3, 7 or 8 can never be a perfect square. So, 198 cannot be written in the form of a perfect square.

7. The one’s digit of the cube of 23 is
(a) 6 (b) 7 (c) 3 (d) 9
Ans. (b) The cubes of the numbers ending with digits 3 have 7 at one’s digit.
So, the one’s digit of the cube of 23 is 7. Also $class 8 maths chapter square and square roots$ .

8. A square board has an area of 144 square units. How long is each side of the board?
(a) 11 units (b) 12 units (c) 13 units (d) 14 units
Ans. (b) Let the side of the square board be “ $x$ ” units. Then the area of the square board = $x^{2}$ units.
Given that area of square board = 144 units
$\Rightarrow x^{2}=144$ units
$\Rightarrow x^{2}=12^{2}$ units
$\Rightarrow x=12$ units
Hence, the length of each side of board is 12units.

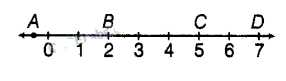
9. Which letter best represents the location of $\sqrt{25}$ on the number line?
(a) A (b)B (c)C (d) D
Ans. (c) C
Since $\sqrt{25}=5$
Therefore, the point “C” on the number line represents $\sqrt{25}$ .

10. If one member of a Pythagorean triplet is 2 $m$ , then the other two members are
(a) $m,m^{2}+1$ (b) $m^{2}+1,m^{2}-1$ (c) $m^{2},m^{2}-1$ (d) $m^{2},m+1$
Ans. (b) $m^{2}+1,m^{2}-1$
For every number $m>1$ , 2 $m$ , $m^{2}+1,m^{2}-1$ form a Pythagorean triplet.

11. The sum of successive odd numbers 1, 3, 5, 7, 9, 11, 13 and 15 is
(a) 61 (b) 64 (c) 49 (d) 36
Ans. (b) We know that, the sum of first $n$ odd natural numbers is $n^{2}$ .
Given odd numbers are 1,3, 5, 7, 9,11,13 and 15.
So, total number of given odd numbers, $n=8$ .
Hence the sum of given odd numbers = $n^{2}=8^{2}=64$ .

12. The sum of first n odd natural numbers is
(a) $2n+1$ (b) $n^2$ (c) $n^2-1$ (d) $n^2+1$
Ans. (b) Consider the following
1 [one odd number] = 1 = $1^2$
1 + 3 [sum of first two odd numbers] = 4 = $2^2$
1 + 3 + 5 [sum of first three odd numbers] = 9 = $3^2$
1 + 3 + 5 + 7 [sum of first four odd numbers ] = 16 = $4^2$
1 + 3 + 5 + 7 + 9 [sum of first five odd numbers ] = 25 = $5^2$
1 + 3 + 5 + 7 + 9 + 11 [sum of first six odd numbers ] = 36 = $6^2$
So we can say that the sum of first n odd natural numbers is $n^2$ .

13. Which of the following numbers is a perfect cube?
(a) 243 (b) 216 (c) 392 (d) 8640
Ans. (b)
216 = 2 x 2 x 2 x 3 x 3 x 3
Grouping the factors in triplets of equal factors, we get 216 = (2 x 2 x 2) x (3 x 3 x 3)
Clearly, in grouping, the factors of triplets of equal factors, no factor is left over.
So, 216 is a perfect cube.

14. The hypotenuse of a right angled triangle with its legs of lengths 3 $x$ x 4 $x$ is
(a) 5 $x$ (b )7 $x$ (c) 16 $x$ (d) 25 $x$
Ans. (a)
Lengths of the legs of the right angled triangle is 3 $x$ and 4 $x$ .
Using Pythagoras Theorem, Hypotenuse = $\sqrt{(3x)^{2}+(4x)^{2}}$
= $\sqrt{9x^{2}+16x^{2}}$
= $\sqrt{25x^{2}}$
= $5x$

15. The next two numbers in the number pattern 1, 4, 9,16, 25,… are
(a) 35, 48 (b) 36, 49 (c) 36, 48 (d) 35, 49
Ans.(b)
We have, 1,4, 9,16, 25, ….
First number of the sequence is = 1= $1^{2}$
Second number of the sequence is = 4= $2^{2}$
Third number of the sequence is = 9= $3^{2}$
Forth number of the sequence is =16 = $4^{2}$
Fifth number of the sequence is = 25= $5^{2}$
Hence, the next two numbers are $6^{2}$ and $7^{2}$ , i.e. 36 and 49.

16.Which among $43^{2},67^{2},52^{2}$ , $59^{2}$ would end with digit 1?
(a) $43^{2}$ (b) $67^{2}$ (c) $52^{2}$ (d) $59^{2}$
Ans. (d)
Since $43^{2}=43\times 43=1849$
$67^{2}=67\times 67=4489$
$52^{2}=52\times 52=2704$
$59^{2}=59\times 59=3481$
Hence square of 59 would end with digit 1.

17. A perfect square can never have the following digit in its one’s place.
(a) 1 (b) 8 (c) 0 (d) 6
Ans. (b)
A number ending with digits 2, 3, 7 or 8 can never be a perfect square. So , a perfect square can never have the digit 8 in its one’s place.

18. Which of the following numbers is not a perfect cube?
(a) 216 (b) 567 (c) 125 (d) 343
Ans.(b)
Prime factorization of 216, 567, 125 and 343 are
216=6 x 6 x 6,
567 = 3 x 3 x 3 x 3 x 7
125 = 5 x 5 x 5,
343 = 7 x 7 x 7
Clearly, 567 is not a perfect cube, because grouping in triplets of equal factors, we are left with two factors 3 x 7.

19. $\sqrt[3]{1000}$ is equal to
(a)10 (b)100 (c)1 (d)none of these
Ans. (a) we know 1000=10 x 10 x 10 .
Taking cube root of both the sides
$\sqrt[3]{1000}$ = $class 8 maths chapter square and square roots$
$\sqrt[3]{1000}$ =10
Hence cube root 1000 is 10 .

20. If $m$ is the square of a natural number $n$ , then $n$ is
(a) the square of $m$ (b) greater than $m$ (c) equal to $m$ (d) $\sqrt{m}$
Ans. (d)
Given that $m=n^{2}$ .
Taking square root of both the side, we get $\sqrt{m}$ = $n$

21. A perfect square number having $n$ digits, where $n$ is even, will have square root with
(a) $n+1$ digit (b) $\frac{n}{2}$ digit (c) $\frac{n}{3}$ digit (d) $\frac{n+1}{2}$
Ans. (b) $\frac{n}{2}$ digit

22. If $m$ is the cube root of $n$ , then $n$ is
(a) $m^{3}$ (b) $\sqrt{m}$ (c) $\frac{m}{3}$ (d) $\sqrt[3]{m}$
Ans. (a)

23. The value of $class 8 maths chapter square and square roots$ is
(a) 14 (b) 12 (c) 16 (d)13
Ans. (c)
$\sqrt{248+\sqrt{52+\sqrt{144}}}$ = $\sqrt{248+\sqrt{52+12}}$
= $\sqrt{248+\sqrt{64}}$
= $\sqrt{248+8}$
= $\sqrt{256}$
=16

24. Given that $\sqrt{4096}=64$ , the value of $\sqrt{4096}+\sqrt{40.96}$ is
(a) 74 (b) 60.4 (c) 64.4 (d) 70.4
Ans. (d) 70.4
$\sqrt{40.96}=\sqrt{\frac{4096}{100}}$
= $\frac{\sqrt{4096}}{\sqrt{100}}$
= $\frac{64}{10}$
=6.4
Hence $\sqrt{4096}+\sqrt{40.96}$ = 64+6.4
=70.4

In questions 25 to 48, fill in the blanks to make the statements true.
25. There are________perfect squares between 1 and 100.
An. 8
There are 8 perfect squares between 1 and 100, i.e. 4, 9,16, 25, 36, 49, 64 and 81.

26. There are________ perfect cubes between 1 and 1000.
Ans.8
There are 8 perfect cubes between 1 and 1000, i.e. 8, 27,64,125, 216, 343 and 729.

27. The unit’s digit in the square of 1294 is________
Ans. 6
We know that, the unit’s digit of the square of a number having digit 4 at unit’s place is 6.
Hence, the units digit in the square of 1294 is 6.

28. The square of 500 will have ……… zeroes.
Ans. 4
Since $500^{2}=500\times 500=250000$
Hence, the square of 500 will have 4 zeroes.

29. There are ………………….. natural numbers between $n^{2}$ and $(n+1)^{2}$ .
Ans. $2n$
Between $1^2$ (=1) and $2^2(=4)$ there are two (i.e., 2 × 1) non square numbers 2, 3.
Between $2^2(=4)$ and $3^2(=9)$ there are four (i.e., 2 × 2) non square numbers 5, 6, 7, 8.
Natural number between $n^2$ and $(n+1)^2$ = $[(n+1)^2-n^{2}]-1$
= $[n^{2}+1+2n-n^{2}]-1$
= $2n$
Hence there are $2n$ natural numbers between the square of $n$ and $n+1$ .

30.The square root of 24025 will have_______digits.
Ans. 3
If number of digits $n$ in any given number is odd , then number of digits in the square root of that number= $\frac{n+1}{2}$
Here $n$ =5
Hence number of digits in the square root of 24025 = $\frac{5+1}{2}$
= $\frac{6}{2}$
=3

31. The square of 5.5 is________
Ans. 30.25
Square of 5.5= $(5.5)^{2}=5.5\times 5.5$
= 30.25

32. The square root of 5.3 x 5.3 is________
Ans. 5.3
Square root of 5.3 x 5.3 = $\sqrt{5.3\times 5.3}$
= $\sqrt{(5.3)^2}$
=5.3

33. The cube of 100 will have________zeroes.
Ans. 6
Cube of 100 = $100^{3}=100\times 100\times 100$
= 1000000

34. $1m^{2}=.........cm^{2}$
Ans. $10000cm^{2}$
$1m^{2}=1m\times 1m$
= $100cm\times 100cm$
= $10000cm^{2}$

35. $1m^{3}=.........cm^{3}$
Ans. $1000000cm^{3}$
$1m^{3}=1m\times 1m\times 1m=100cm\times 100cm\times 100cm$
= $1000000cm^{3}$

36. One’s digit in the cube of 38 is________
Ans. 2
Since $38^{3}=38\times 38\times 38$
=54872

37. The square of 0.7 is________
Ans: 0.49
Square of 0.7 = $0.7^{2}=0.7\times 0.7$
=0.49

38. The sum of first six odd natural numbers is________
Ans. 36
Since sum of first ‘ $n$ ‘ odd natural numbers = $n^{2}$
So, sum of first ‘6’ odd natural numbers = $6^{2}$
=36

39. The digit at the one’s place of $57^{2}$ is________
Ans. 9
Since the unit’s digit of a square of a number having digit at unit’s place as 3 or 7 is 9.
So the digit at the one’s place of $57^{2}$ is =9

40. The sides of a right triangle whose hypotenuse is $17 c m$ are _________ and _________.
Ans: $8$ $15$ $15$ Then $m^{2}=17-1=16$
This implies $m$ =4.
Therefore, the required triplet is 2 $m$ = $2\times 4=8$ , $m^{2}-1=4^{2}-1=15$ and 17 . $2 m, m^{2} - 1, m^{2} + 1$

41. $\sqrt{1.96}=......$
Ans: 1.4
$\sqrt{1.96}=\sqrt{\frac{196}{100}}=\frac{\sqrt{196}}{\sqrt{100}}=\frac{14}{10}=1.4$

42. $(1.2)^{3}=...........$
Ans. 1.728
$(1.2)^{3}=1.2\times 1.2\times 1.2=1.728$

43. The cube of an odd number is always an _________ number.
Ans: always an odd number

44. The cube root of a number $x$ is denoted by _________.
Ans. $\sqrt[3]{x}$

45. The least number by which $125$ be multiplied to make it a perfect square is ……..
Ans. 5
Prime factorization of $125 = 5 \times 5 \times 5$ On grouping these factors in pair of equal factors, $125 = 5 \times 5 \times 5$ e have only one $5$ without a pair. So, $125$ to be multiplied by $5$ to make it a perfect square.

46. The least number by which 72 be multiplied to make it a perfect cube, is________
Ans. 3
Prime factorization of 72 is
72=2 x 2 x 2 x 3 x 3
Grouping the factors in triplets of equal factors, we get
$72=\underline{2\times 2\times 2}\times 3\times 3$
It is clear that 2 occurs as a prime factor of 72 thrice, but 3 occurs as a prime factor only twice. Thus, if we multiply 72 by 3, 3 will also occurs as a prime factor thrice and the product will be $72=\underline{2\times 2\times 2}\times\underline{3\times 3\times 3}$ , which is a perfect cube.
Hence, the least number, which should be multiplied with 72 to get perfect cube, is 3.

47. The least number by which 72 be divided to make it a perfect cube, is________
Ans. 9
Prime factorization of 72 is
72=2 x 2 x 2 x 3 x 3
Grouping the factors in triplets of equal factors, we get
$72=\underline{2\times 2\times 2}\times 3\times 3$
Clearly, if we divide 72 by 3 x 3, the quotient would be 2 x 2 x 2, which is a perfect cube. Hence, the least number by which 72 be divided to make it, a perfect cube, is 9.

48. Cube of a number ending in 7 will end in the digit________
Ans. 3
The cubes of the numbers ending in digit 7 ends in digit 3.
For example: 7 x 7 x 7 = 343 , 17 x 17 x17 = 4913 etc.

True/False
In questions 49 to 86, state whether the statements are True or False.
49. The square of 86 will have 6 at the unit’s place.
Ans. True
The unit’s digit of the square of a number having digit at unit’s place as 4 or 6 is 6.

50. The sum of two perfect squares is a perfect square.
Ans. False
e.g. 16 and 25 are the perfect squares, but 16 + 25 = 41 is not a perfect square.

51. The product of two perfect squares is a perfect square.
Ans. True

52. There is no square number between 50 and 60.
Ans. True
Numbers between 50 and 60 are 51,52, 53, 54, 55, 56, 57, 58 and 59.
It is clear that there is no square number between 50 and 60.

53. The square root of 1521 is 31.
Ans. False
Because $31^{2}=961$ .

54. Each prime factor appears 3 times in its cube.
Ans. True

55. The square of 2.8 is 78.4.
Ans. False
Since $(2.8)^2=2.8\times 2.8=7.84$

56. The cube of 0.4 is 0.064.
Ans. True
As $(0.4)^3=0.4\times 0.4\times 0.4=0.064$

57. The square root of 0.9 is 0.3.
Ans. False
As, the square of 0.3 = (0.3)² = 0.3 x 0.3 =0.09

58. The square of every natural number is always greater than the number itself.
Ans. False
1 is a natural number and square of 1 is 1 which is equal to itself.

59. The cube root of 8000 is 200.
Ans. False
Cube root of 8000 is 20.

60. There are five perfect cubes between 1 and 100.
Ans. False
There are eight perfect cubes between 1 and 100, i.e. 8, 27, 64, 125, 216, 343, 512 and 729.

61. There are 200 natural numbers between $100^2$ and $101^2$ .
Ans. True
$100^2=10000$
$101^2=10201$
Natural numbers s between $100^2$ and $101^2$ .
Natural number between 10000 and 10201= 10201-10000-1=200.

62. The sum of first n odd natural numbers is $n^2$ .
Ans. True

63. 1000 is a perfect square.
Ans. False
1000 = 2 x 2 x 2 x 5 x 5 x 5 = 2 ² x 5²x 2 x 5
Since there are two unpaired factors 2 and 5 , so it is not a perfect square.

64. A perfect square can have 8 as its unit’s digit.
Ans. False

65. For every natural number $m$ , ( $2m-1$ , $2m^3-2m$ , $2m^2-2m+1$ ) is a Pythagorean triplet.
Ans. False
$15$

66. All numbers of a Pythagorean triplet are odd.
Ans. False
Since $3^2+4^2=5^2$ . Hence 3,4, and 5 are Pythagorean triplet but 4 is an even number.

67. For an integer $a$ , $a^3$ is always greater than $a^2$ .
Ans. False
-2 is an integer and $(-2)^3=-8$ which is less than $(-2)^2=4$ .

68. If $x$ and $y$ are integers such that $x^2>y^2$ , then $x^3>y^3$ .
Ans. False
Suppose , -1 and -2 are integers , then $(-2)^2>(-1)^2$ but $(-2)^3=-8$ which is less than $(-1)^3=-1$ .

69. Let $x$ and $y$ be natural numbers. If $x$ divides $y$ , then $x^3$ divides $y^3$ .
Ans. True
Let $x$ and $y$ be natural number such that $x$ divides $y$ , then $y=kx$ .
$\Rightarrow y^3=(kx)^3$
$\Rightarrow y^3=k^3x^3$
$\Rightarrow x^3$ divides $y^3$ .

70. If $a^2$ ends in 5 , then $a^3$ ends in 25.
Ans. False
$(35)^2=1225$ end in 5 and $(35)^3$ = 42875 does not end in 25 .

71. If $a^2$ ends in 9, then $a^3$ ends in 7.
Ans. False
$7^2=49$ ends in 9 and $(7)^3=343$ does not end in 7.

72. The square root of a perfect square of $n$ digits will have $\frac{n+1}{2}$ digits, if $n$ is odd.
Ans: True.
As 10000 is a perfect square with 5 digit then its square root which is equal to 100 has $\frac{5+1}{2}=\frac{6}{2}=3$ digits .